I work a lot with and on a particular piece of software called MMT, which was developed by Florian, so this is my attempt to explain what it does – which is not exactly easy, as you’ll see, but one of the things you can do with MMT is make computers (on some level) understand math, so here’s how that works:
MMT used to stand for Module system for Mathematical Theories, but by now Florian prefers the acronym to stand for Meta-Meta-Tool or Meta-Meta-Theory (which is probably more accurate, since by now math is only one of its domains of application).
MMT consists of two parts: A formal language (OMDoc/MMT) and a corresponding software and API for managing documents in that language, so I’ll first explain how the former works and then what the latter is capable of.
(A slightly more technical introduction to MMT can be found here)
The OMDoc/MMT Language
OMDoc/MMT is a description language based on OpenMath, a simple XML-based language to describe mathematical expressions with respect to their semantics. Exemplary, the expression \(\sin(x)\) in OpenMath would look like this:
<OMOBJ>
<OMA>
<OMS name="sin" cd="transc1"/>
<OMV name="x"/>
</OMA>
</OMOBJ>
The OMA stands for an application of a symbol, OMS for a previously declared symbol in some content dictionary (i.e. a document declaring new symbols, given by the cd=…-tag) and OMV represents a variable. Expressions like these are called objects in OpenMath (hence the OMOBJ tag).
The advantage of OpenMath when compared to other description languages like LaTeX (which of course, is solely for presentation and thus not directly comparable) is, that it distinguishes between symbols with the same notation. For example, the composition of two functions \(f,g\) is usually denoted by \(f\circ g\) – however, so is the composition of two arbitrary elements \(f,g\) of some general monoid/group etc. In OpenMath, function composition and monoid composition are two distinct symbols, even though they are denoted the same way. By contrast, in LaTeX for example both are just expressed as f\circ g with no information, what f,g and \circ actually mean.
Furthermore, the content dictionaries can (and should) not just declare the symbols, but also provide their definitions and additional information (such as examples). This is what the entry for the logarithm looks like in its OpenMath content dictionary:
<CDDefinition>
<Name> log </Name>
<Description>
This symbol represents a binary log function; the first argument is
the base, to which the second argument is log'ed.
It is defined in Abramowitz and Stegun, Handbook of Mathematical
Functions, section 4.1
</Description>
<CMP>
a^b = c implies log_a c = b
</CMP>
<FMP>
<OMOBJ>
<OMA>
<OMS cd="logic1" name="implies"/>
<OMA>
<OMS cd="relation1" name="eq"/>
<OMA>
<OMS cd="arith1" name="power"/>
<OMV name="a"/>
<OMV name="b"/>
</OMA>
<OMV name="c"/>
</OMA>
<OMA>
<OMS cd="relation1" name="eq"/>
<OMA>
<OMS cd="transc1" name="log"/>
<OMV name="a"/>
<OMV name="c"/>
</OMA>
<OMV name="b"/>
</OMA>
</OMA>
</OMOBJ>
</FMP>
</CDDefinition>
…where CMP is the defining mathematical property of the symbol in natural language and FMP the same property expressed as an OpenMath object. That way, every usage of a symbol is intrinsically linked to its definition, and (if possible) the definition itself is expressed formally in OpenMath – this is a big step towards linking mathematical expressions to their actual semantics.
Michael then extended OpenMath to not just cover mathematical formulae, but actual mathematical documents – the result was OMDoc, adding features such as definitions, theorems, proofs, examples etc. and additional narrative structure: It (in theory) allows for describing the content and structure of arbitrary formal documents such as papers, textbooks, lecture notes etc. OMDoc introduces the following three leveled knowledge structure:
- Object level: formulae (as in OpenMath) are OMDoc objects.
- Statement level: OMDoc statements are named objects of a certain type (definition, theorem,…).
- Theory level: OMDoc statements are collected in theories, which are backwards compatible to OpenMath content dictionaries.
Additionally, OMDoc adds various way to connect theories via morphisms, giving rise to the notion of a theory graph. For example, theories can simply import other theories (making the contents of the imported theory available to the importing theory). Other morphisms can act like imports but change names or other properties of the imported symbols, or simply map statements in one theory to mathematical expressions over the contents of another theory:
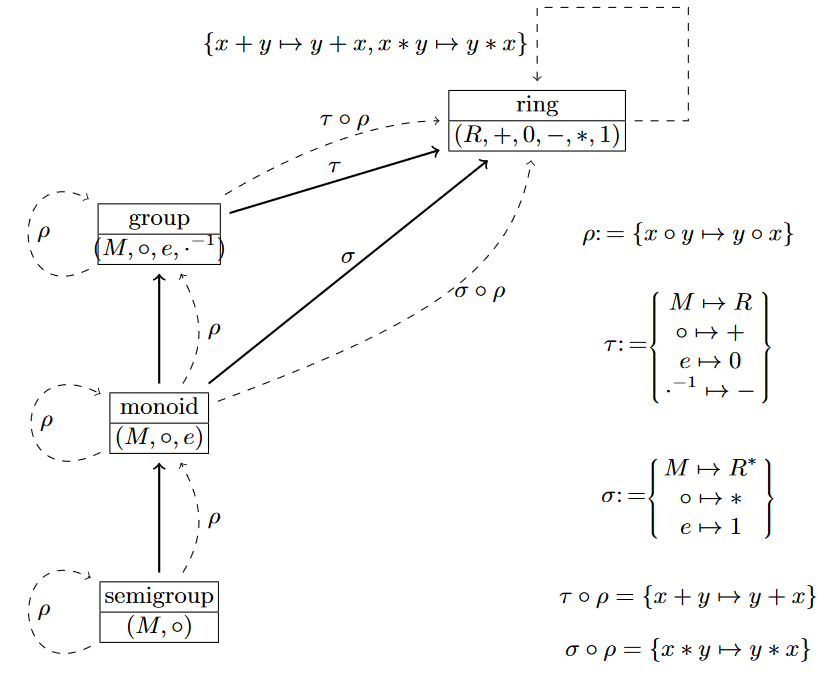
The above theory graph shows the development of the theory of rings – a ring has two ingoing morphisms \(\tau\) and \(\sigma\), the former for the additive group of the ring, the latter for its multiplicative monoid. Additionally, the theory of groups inherits (i.e. imports) from the theory of monoids, which in turn extends the theory of semigroups.
Now, why are theory graphs useful? Because they allow us to build theories according to the little theories approach. The inheritance arrows between theories allow us to also inherit provable results, without the need of reproving them again – just as we do it in mathematical practice. If I know that a ring is a group, I know every result that holds for groups in general also holds for rings. If I know a group is a monoid, I know everything that holds for monoids also holds for groups. It allows me to state (and prove) everything on the most general level.
Finally, MMT/OMDoc is just a slight adaption of OMDoc, most prominently it introduces the notion of a constant on the statement level. A constant is a named symbol with (optionally) a “type” object, a “definition” object and additional information such as its notation and what role the constant plays in a larger context (e.g. equality or simplification rule).
However, MMT/OMDoc still does not fix any meaning to the words type or defintion – it is still just a description language without any inherent rules. The same holds for theories – they are just collections of declarations without any fixed semantics. In Florian’s terms, MMT is foundation independent. That’s because MMT/OMDoc strives to be general enough to capture the (abstract) syntax, semantics and proof theory of any arbitrary formal language (in addition to the narrative elements of documents).
Of course, nobody would want to write OMDoc files by hand – which is why MMT adds a surface language, that allows for creating MMT/OMDoc documents more easily. As an example, the following is a valid document in MMTs surface syntax:
namespace http://cds.omdoc.org/example GS theory Foo : ur:?LF = Nat : type US # ℕ RS plus : ℕ → ℕ → ℕ US # 1 + 2 RS GS
“Compiled” into OMDOc, the above code would yield this:
<omdoc>
<theory name="Foo" base="http://cds.omdoc.org/example"
meta="http://cds.omdoc.org/urtheories?LF">
<constant name="Nat">
<type><OMOBJ>
<OMS base="http://cds.omdoc.org/urtheories" module="Typed" name="type"/>
</OMOBJ></type>
<notations>
<notation dimension="1" fixity="mixfix" arguments="ℕ"/>
</notations>
</constant>
<constant name="plus">
<type><OMOBJ>
<OMA>
<OMS base="http://cds.omdoc.org/urtheories" module="LambdaPi" name="arrow"/>
<OMS base="http://cds.omdoc.org/example" module="Foo" name="Nat"/>
<OMS base="http://cds.omdoc.org/example" module="Foo" name="Nat"/>
</OMA>
</OMOBJ></type>
<notations>
<notation dimension="1" fixity="mixfix" arguments="1 + 2"/>
</notations>
</constant>
</theory>
</omdoc>
A more comprehensive description of both MMTs surface language as well as the abstract language of OMDoc/MMT can be found here.
The nice thing about MMTs surface syntax is, that – as in the example above – we can attach notations to our constants, that mirror the notations that are actually used in mathematical practice and which we can then use to write formulae. Notations also allow for implicit arguments, which again mirror mathematical practice and are quite convenient.
Suppose, we wanted to give an operator for declaring some function to be injective. The type of such an operator would be something like
\[\text{injective: } \prod_{A:\text{type}}\prod_{B:\text{type}}\prod_{f:A\to B}\text{prop}.\]
It takes the domain \(A\) and codomain \(B\) of a function, the function \(f\) itself and returns the proposition, that \(f\) is injective. The operator has to take domain and codomain as argument, because otherwise I can’t even state the (required) type of the argument function \(f\). But if I know the type of \(f\), I also know the domain and codomain – stating them each time I want to declare a function as injective would be most annoying, so I can give \(\text{injective}\) a notation # 3 is injective, which only uses the third argument and thus leaves the first and second one implicit (and thus to be inferred by the MMT system, ultimately). Now if I have a function \(f\) around, I can just write f is injective and I’m done.
The MMT System
So, the question remains, what we can do with OMDoc/MMT documents – after all, just having the language itself is rather pointless. This is where the MMT system comes into play.
At its core, MMT is an API written in Scala (which compiles into .class files and hence is “backwards compatible” with Java) – i.e. a library of classes and functions related to OMDoc content. At its center, it has an (executable) controller, that provides various user interfaces and is extended by arbitrary plugins providing various features and commands. This plugin architecture allows MMT to be highly generic and extensible, and all of its core classes are attempted to be implemented modularly and in various stages of abstraction, to make adding additional features and support for new systems and languages as easy and convenient as possible. A comprehensive description can be found here, so I’ll restrict myself to a list of things MMT provides and what they can be (and are) used for:
- A backend that manages OMDoc/MMT libraries and stores/reads them into memory from various sources (files, databases etc.).
- A build system, that takes documents in some format and converts them to (primarily, but not necessarily) OMDoc files, separating its contents into the actual (semi-formal) content, its narrative structure in the original document and all relational information (i.e. how all the modules relate to each other via theory morphisms like inclusions).
- This is managed via an abstract class Importer, that combines a parser and an (optional) type-checker for any arbitrary formal language and returns well-formed OMDoc elements; the build manager then handles all the input and output, the archive structure, keeping track of dependencies, the communication with the backend etc.
Standard implementations for a parser are the one for MMTs surface syntax and one for the Twelf syntax, but by now we also have one for (mostly xml-exports of) the Mizar, HOLLight and PVS systems.
The type checker is also implemented as generically as possible, so that all a user needs to do is implement the checking rules and none of the algorithmic “boilerplate” stuff – exemplary, we have a checker for the logical framework LF, whose implementation (basically) just consists of a scala object for each of the inference rules of the \(\lambda\Pi\)-calculus.
I implemented extensions of the latter by standard type constructors (\(\Sigma\)-types, coproducts, finite types,…) up to a logical framework based on homotopy type theory – in each case by just implementing the rules alone as separate scala objects. Building a logical framework / foundational logic couldn’t be more convenient 🙂 - A theorem prover, which similarly to the type checker can be supplied with foundation-dependent rules. It’s not even remotely comparable to state-of-the-art theorem provers (which, I guess, it can’t reasonably expected to), but works surprisingly well for “trivial” things, and can of course – as a general class – be used as a basis to implement your own algorithm.
- A shell which can be used as a frontend to issue commands (e.g. building) to the MMT system.
- An IDE in the form of a jEdit-Plugin, which offers syntax highlighting, auto-completion and access to the shell.
- A server which can be used to browse and present the contents of available archives
- A presenter-class that outputs available content as e.g. text, html, latex… (the html presenter is e.g. used by the server, the text presenter by the shell)
So basically, the MMT system can be used as a generic “engine” to conveniently and quickly implement arbitrary formal systems without the developer having to care about all the boilerplate stuff that isn’t part of the purely formal specification of the system. Everything works via plugins, so adding new features, imports or instances of any of the above abstract features is intended to be as convenient as possible.
Furthermore, it can serve as a common framework for various different systems – if you consider my Ph.D. topic, you’ll notice that this is pretty much the perfect system to work on knowledge management across different formal libraries – once I have import methods for all the systems I want to work on, I have a common system in which to talk about and access all of them at once. And it allows for implementing features such as expression translation, identification of content overlap etc. on an extremely generic level.
Which ultimately is exactly what MMT wants to be – in every aspect as generic as possible.
[…] 1. I love how he calls the limit definition “ill-defined” and then gives an (apart from the error above) rigorous, formal definition in first-order logic. Seriously, you can’t make something more well-defined than by using first-order logic. I mean, that’s kind-of what first-order logic is for! You can even input this definition in an automated theorem prover and see that it checks out. Just for fun, I did exactly that in our own MMT system: […]